6. Mixed complementarity problems#
Before delving deeper into how the complex relations between the actors affect the outcome of the electricity/commodities markets, it is first necessary to set a solid foundation. First, we will discuss some basic concepts in game theory, such as Pareto efficiency and Nash and Nash-Cournot games. Secondly, we will briefly describe the fundamentals of Mixed Complementarity before we discover their relevance to study energy markets.
6.1. Game theory basics#
So far, we have considered the dispatch of power from the system perspective, i.e, how would a central planner dispatch the available power plants in the most cost-efficient way. This assumes that this central planner has full control of and information on these power plants. Modern, liberalized electricity systems do not work in such a centralized manner, but are rather market-based, meaning that a large set of actors (e.g., producers, consumers) are involved. These actors act in a selfish manner to maximize their profits or utility.
To model the behavior of different actors in the market, it is necessary to employ a mix of optimization and game theory. Let’s begin with one of the classic game theory examples, the Prisoner’s Dilemma. Assume that two suspected bank robbers, Thelma & Louise, are captured by the police. They are separated and have the choice of whether or not to confess and implicate the other:
if both confess, they both serve 10 years in jail;
if one confesses and implicates the other and the other doesn’t, she goes free, the other serves 20 years;
if none of them confess, they both serve 1 year.
The payoff matrix of the prisoner’s dilemma can be seen in Table 6.1. Based on the payoff matrix, the optimal scenario is for neither Thelma nor Louise to confess, as this leads to less years in prison in total. This situation of the payoff matrix (1,1) is the Pareto-optimal outcome of the prisoner’s dilemma.
On the contrary, the Nash equilibrium of the dilemma is when both Thelma and Louise confess, and each serves 10 years in prison. The presented example is a case of a “non-cooperative game” where Thelma and Louise selfishly try to maximize their own utility
Thelma confesses |
Thelma does not confess |
|
|---|---|---|
Louise confesses |
(10, 10) |
(20, 0) |
Louise does not confess |
(0, 20) |
(1, 1) |
Linking this back to our example, the case where both Thelma and Louise confess is the Nash equilibrium point since Thelma has no utility if she changes her strategy unilaterally. If she chooses to not confess, instead of 10 years in prison, she will receive 20 years while Thelma will be released. In other terms, her utility will be lower than the Nash-equilibrium point. In summary, in Nash games, each actor chooses the strategy with the highest payoff for themselves, assuming that the other actors have done the same at the same time [Gabriel et al., 2013].
Such Nash games can be used to describe perfectly competitive electricity markets, where the producers and consumers are price-takers. This means that the market actors do anticipate how their own actions will influence the market price. In contrast, in Nash-Cournot games, each firm anticipates its impact on the market through the knowledge of the inversion function [Ruiz et al., 2014]. More specifically, in a Nash-Cournot game, the firms compete on production quantity and anticipate the impact of their own actions on the commodity price.
Pareto Optimal Outcome
The Pareto optimal strategy, named after the economist Vilfredo Pareto, corresponds to a strategy, where no alternative one exists, that benefits all actors. Therefore, it is the optimal solution for all actors jointly.
6.2. Basics of mixed complementarity problems#
Let’s assume a general optimization problem, as seen below :
The Lagrangian reads :
:label: eqn:Lagrangian
The KKT conditions of the problem are the following :
:label: eqn:KKT
The set of KKTs described in equation (4.18) are an instance of a Mixed Complementarity Problem. Because for linear and convex quadratic (non-linear) optimization problems, the KKT pose both a sufficient and necessary condition for optimality, the solution of the MCP satisfies the KKTs of the original problem and therefore is a solution. In the following paragraphs, we will examine how MCPs can help us solve market clearing problems from the perspective of market actors.
Note
According to [Gabriel et al., 2013] a Non Linear Complementarity problem is defined as : If we have a function
The Mixed Complementarity problem is a generalization of the NCP, as it allows for variables with both upper and lower limits
6.3. Application of mixed complementarity problems in electricity markets#
Let’s start with a simple market clearing problem. The market-clearing problem is relevant to pool-like market. In such a pool, the market operator has to clear the auction and decide on a market price along with quantities from each producer. Once again, the market clearing problem is from the side of the pool/system operator, which aims at maximizing social welfare. The optimization problem is considered under given price-quantity pairs of supply and demand agents,
The KKT conditions of the market-clearing problem (6.4) are :
Now let’s look at the issue from the side of the supply and demand agents participating in the electricity market, offering price-quantity pairs. These, contrary to what presented up to now, have to be decided by each participant. So what is the optimization problem faced by the suppliers (generators) and the demand agents (customers, retailers) ?
First, the generators wants to maximize their profit given the market clearing price. As we are discussing the problem in the context of a perfectly competitive market, there is enough supply that the actions of individual do not influence the market price. Therefore, bridging with the previous chapter, supply and demand agents compete in a Nash game. In that case, the market clearing price
where :
The KKT conditions of the problem (6.6) are the following :
Secondly, the demand agents aim to maximize their utility, again by using the assumption that their actions do not influence the market price. Therefore, the optimization problem faced by the demand-side agents is :
where :
The KKT conditions of the problem (6.8) are :
The two different optimization problems are connected through a common linking constraint, requiring supply and demand quantities to match. That is constraint (2) of the initial market clearing problem. To arrive at the equilibrium of the Nash game between demand and supply agents we need to simultaneously solve the supply-side problem (6.6), the demand-side problem (6.8) and the linking constraint (2) of problem (6.4).
There are several ways to solve the new optimization problem. We can follow one of the three methods :
Concatenate the optimality conditions from the KKTs of the individual problems ((6.6), (6.8)) along with the linking constraint to form a Mixed Complimentarity Problem. We will later show, why by concentating the constraints we arrive at the MCP. Then the MCP can be solved either with dedicated solvers such as PATH or as a feasibility problem( NLP, MIPL, optimization problems).
Apply price-search algorithms and iterative methods, to find a solution that satisfies all costraints.
Derive an equivalent optimization problem (EOP) and solve it using optimization solvers, such as yalmip used during the course.
But now let’s prove why concatenating the KKT conditions of problems ((6.6), (6.8)) along with the linking constrait formulates an MCP.
Comparing the KKTs of the concatenated problem (6.10) with those of the market-clearing problem (6.4), we can deduce that there is a difference in the following constraints :
But since we know that in electricity markets suppliers bid their capacity at variable cost and demand agents at their willigness to pay, we can conclude
Warning
Every optimization has an equivalent MCP, but not every MCP has an equivalent optimization problem.
6.3.1. An alternative formulation of the market clearing problem#
Another formulation of the Nash game between demand and supply agents can be presented through the use of an inverse demand function. In that case, instead of having demand bid-pairs, a linear relationship between the price of electricity and the demanded quantity is in place. The linear equation takes the form of :
But since from the linking constraint we know
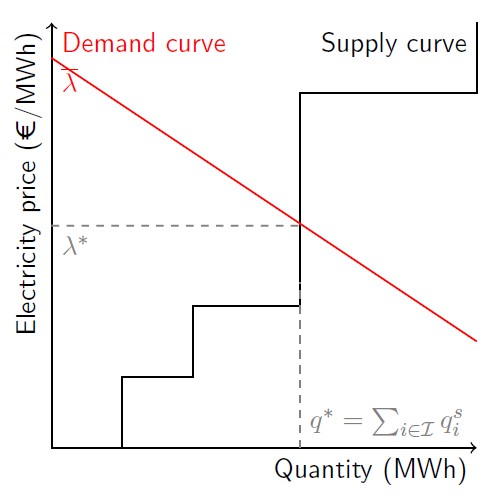
Fig. 6.1 Inverse demand function and supply curve, based on supply-side bid pairs.#
Calculating the KKT conditions of the game yields the MCP. Note that the inverse demand function participates as-is in the MCP, but is not part of the optimization problem (it is outside of the curly brackets). That is the case since we are participating in a Nash game, and therefore the suppliers do not consider their actions impact on price !
With the MCP defined, we can now derive the Equivalent Optimization problem to solve the initital game (6.13). Remember here, that the KKT conditions of the EOP and the MCP have to be the same in order for the EOP to provide a solution to the initial problem. To derive the EOP we make use of the graphical interpretation of the problem show in Fig. 6.1. Remember here, that the we proved that the Nash game is equivalent to the market-clearing problem faced by the market operator. Leveraging this, we can derive the EOP to maximize the Social Welfare. Based on Fig. 6.2 and the fact that the social welfare is the area under the supply and the demand curves we can say that :
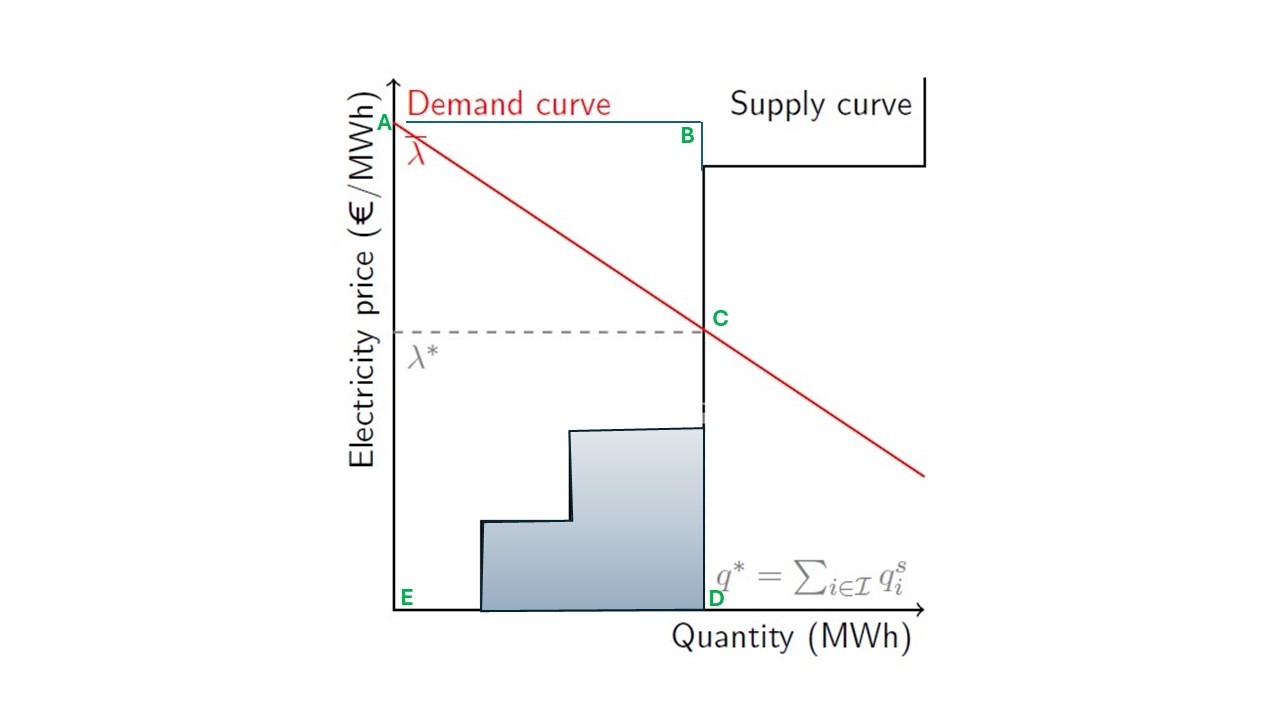
Fig. 6.2 Areas to calculate social welfare from inverse demand and supply curves.#
Therefore the EOP is formulated as :
Finally, the equivalence of the MCP with the EOP can be demonstrated through the derivation of the KKTs for the EOP (6.15).
6.3.2. Nash-Cournot games#
Up to now, we have assumed a perfectly competitive market, meaning firms have zero market power and act as pure price-takers. This is only a theoretical artefact, as firms always have some market power. To model such interactions, a Nash-Cournot game can be implemented, where each agent assumes that the impact of the other players decision on the price is given. Therefore, he acts on the the residual demand. Again, we will make use of an inverse demand curve to simulate the demand-side bids. Now that the impact of the other players decision is part of the optimization problem of a single agent, the inverse curve is part of the optimization problem. The Nash-Cournot game is present below :
Warning
In the Nash-Cournot game the inverse demand function is now an integral part of the optimization problem.
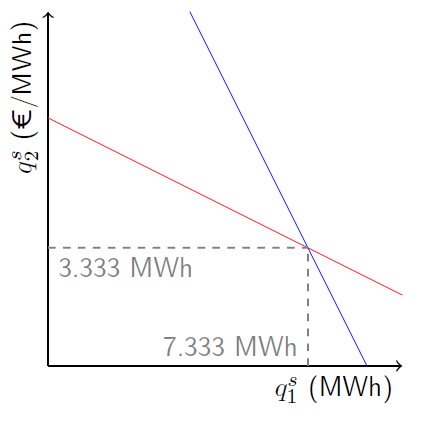
Now to better understand how to solve a Nash-Cournot game, we will walk through a numerical example. Let us assume two market participants that compete a la Cournot. The demand is elastic and described by and inverse demand function with
When there is competition between two agents, an easy way to find the equilibrium point is through a graphical solution, as illustrated in (6.16). To obtain the graphical solution, we solve the problem for supplier 1, by derivating the objective function w.r.t
Overall, the Nash-Cournot games can be solved with similar methods to Nash games, by either:
concatenating the optimality conditions and linking constraints to form an MCP, which can be solved graphically or through variable algorithms
through iterative price search algorithms
through the derivation of an Equivalent Optimization Problem, which can be solved through optimization algorithms
How can the EOP be obtained in the case of a la Cournot competition ? As always, let us start through deriving the KKT conditions for a generalized Nash-Cournot game (6.16):
Now comparing the Lagrangian between the Nash game (10a) and Nash-Cournot game (10a’) we see the following difference. The Nash-Cournot game has an extra term of
Finally, some remarks on the Equivalent Optimization Problem of the Nash-Cournot game with the inverse demand function. Firstly, the objective function of the does not compute some direct measure of the Social Welfare expected by clearing the market, in comparison to the Nash game. The objective function of the EOP is a mere artefact constructed to solve the Nash-Cournot game. Secondly, despite the non-linear terms (squared) of the EOP, we are still in the convex optimization region and therefore can obtain a solution to the problem through the KKTs.
6.4. Remarks#
With the introduction of the Mixed Complementarity problems as a way to solve the Nash and Nash-Cournot games, we have introduced a paradigm shift in the way we study the market interactions. Up to now, we were considering the market only from the side of a pool operator that aims to clear the market. Now, with the new tools available we can model the market clearing along with the interactions between different market actors. Specifically, through the Nash equilibrium we can model the participation of agents in a perfectly competitive market, where they have zero market power. Moreover, to formulate a problem that better describes modern market, we introduced the Nash-Cournot equilibrium. In a Nash-Cournot game, the actors have market-power and try to optimally set their actions, considering the actions of the other actors as granted.
For both Nash and Nash-Cournot games, we demonstrated how through the formulation of a Mixed Complementarity Problem, which has equivalence of the KKT conditions, and then solve an Equivalent Optimization Problem, to find the equilibrium solution. For the Nash game, we showed that the Equivalent Optimization Problem is the maximization of the social welfare, as exactly in the market clearing problem. Finally, we also extracted the Equivalent Optimization Problem for the Nash-Cournot game, based on comparing the Nash-Cournot with the Nash game KKTs. All in all, through the use of equilibrium problems we can make relationships and interactions between market agents explicit, and have a more intuitive way of formalizing problem. Through the tools of MCP and EOP we can solve these equilibrium problems!
6.5. References#
Steven A. Gabriel, Antonio J. Conejo, J. David Fuller, Benjamin F. Hobbs, and Carlos Ruiz. Complementarity Modeling in Energy Markets. Springer New York, New York, NY, January 2013. doi:10.1007/978-1-4419-6123-5.
Carlos Ruiz, Antonio J Conejo, J David Fuller, Steven A Gabriel, and Benjamin F Hobbs. A tutorial review of complementarity models for decision-making in energy markets. EURO Journal on Decision Processes, 2:91–120, 2014.